Passwortsicherheit, Länge, Komplexität

Die Sicherheit von Passwörten ergibt sich aus dem Aufwand den jemand betreiben muss um das Passwort herauszufinden. Eine Methode die sicher immer funktioniert ist der Brute-Force Angriff. Das ist nichts anderes als das konsequente durchprobieren aller möglichen Zeichenkombinationen. Man erzeugt der Reihe nach ale möglichen Passwörter und berechnet jeweils einen Hash-Wert dazu. Diesen vergleicht man. Für die Hashberechnung gibt es verschiedene Verfahren deren Berechnungsaufwand unterschiedlich ist. Eine weitere Einflussgrösse ist die Rechenleistung mit der man diese Hash-Berechnungen und Vergleiche durchführen kann.

Die Passwortlänge ist entscheidend, Sonderzeichen bringen wenig

Die Anzahl möglicher Kombinationen die man durchprobieren muss hängt von der Passwortlänge und der Zeichenraumgrösse ab, also von der Anzahl möglicher Zeichen die im Passwort verwendet sein können. Mit Gnuplot kann man diese Anhängigkeit gut darstellen:

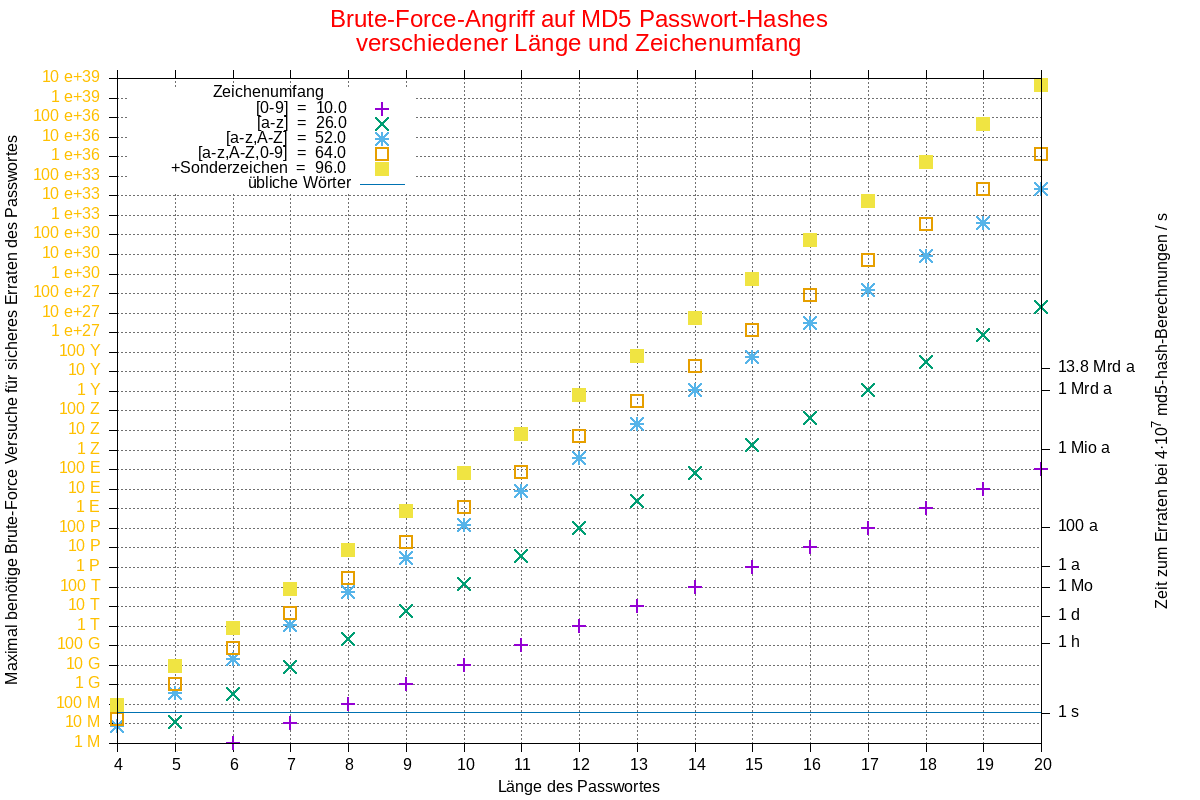
Vertikal ist der Aufwand in Form der erforderlichen Rechenoperationen zur sicheren Lösung aufgetragen, in X-Richtung ist die Passwortlänge aufgetragen, und als Parameter sind die üblicher Weise in Frage kommenden Zeichenräume gegeben. Sehr schön ist zu sehen, dass die Passwortlänge die Sicherheit deutlich stärker erhöht als eine erweiterter Zeichenraum. Zum Beispiel: Das Sicherheitsniveau eines Passwortes mit 10 Zeichen aus einem Zeichenraum von [a-z,A-Z,0-9] (64 Zeichen) kann man ebenso mit einem Zeichenraum aus nur [a-z] (26 Zeichen) erreichen in dem man das Passwort 3 Zeichen länger macht. Die häufige Empfehlung in jedem Fall einen grossen Zeichenraum (Sonderzeichen) zu verwenden ist also eine Fehleinschätzung.

Was kostet es den Angreifer?

Der Aufwand für einen Passwortbruch lässt sich auch in Form von Kosten darstellen, die für das Ausprobieren anfallen. Dabei ist angenommen, dass mit einem PC mit einer GPU gearbeitet wird das dann bei Vollast 500 W Leistung verbraucht und so einschliesslich Abschreibung der Anschaffung über 5 Jahre ca 4,– EUR Kosten pro Tag anfallen. Die Rechenleistung eines solchen PC+GPU Kombination liegt heute in der Grössenordnung von 35 Millionen Hashes / s (MD5). Damit ergeben sich dann folgende Kosten:

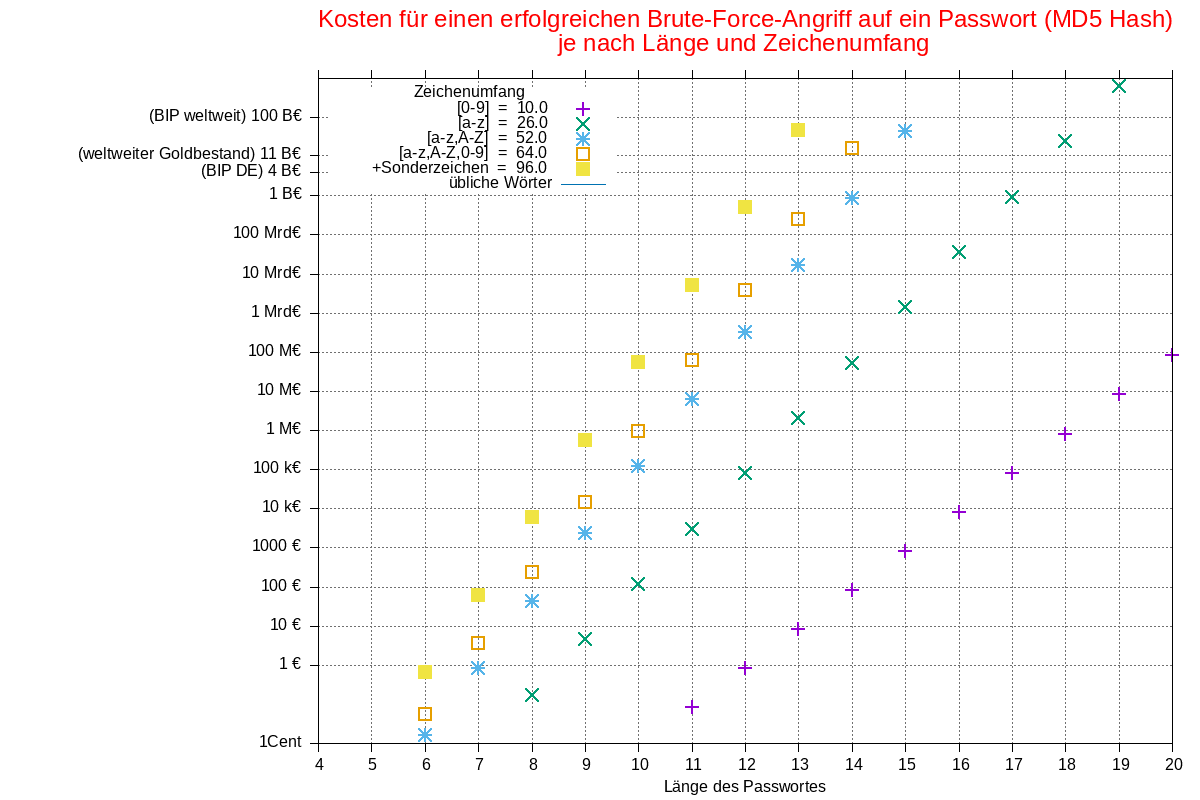
Daraus sieht man klar: Brute-Force lohnt sich nur bei sehr geringen Passwortlängen, jenseits von 11 Stellen wird der finanzielle Aufwand sehr gross. Bei den sich ergebenden gigantischen Zahlen fehlt einem die Vorstellung, deshalb habe ich ein Paar Beispiele für grosse €-Summen an die Skala aufgetragen.

Es bleibt zu beachten, dass Rechnersysteme ständig leistungsfähiger werden und die zeitliche und finanzielle Skala sich damit verschieben. Sogenannte Supercomputer können heute in der Grössenordnung von 50 Billiarden (50×10¹⁵) Hash-Berechnungen pro Sekunde ausführen. Das verschiebt zwar die Zeitskala um 6 Grössenordnungen, allerdings sieht die Kosteneffizienz dabei nicht so viel besser aus. Das bedeutet, man braucht ca. 4…6 Zeichen mehr um auch vor Angriffen mittels Supercomputer (NSA? GHCQ?) geschützt zu sein. Das verwenden von 16…20 Zeichen für Passwörter ist garnicht so absurd wie der erste Blick auf die Grafik suggerieren könnte. Nur noch zum Vergleich: das Bitcoin-Netzwerk wird mit einer Leistung von 69×10¹⁸ SHA256 Hashes/s (2019) angegeben. Das kann man zwar nicht einfach mal so zum Passwortknacken umfunktionieren, zeigt aber den Horizont der Möglicheiten.

Die Menschliche Komfort-Falle

Bequemlichkeit ist bekanntlich der häufigste Schwachpunkt der meisten Menschen, auch wenn es um Sicherheit geht. Entsprechend häufig werden Namen oder simple Zeichenfolen (123456) als Passwörter verwendet. Das ist mit einem Wörterbuchangriff ausnutzbar. Ein solcher führt aber nicht sicher zu einem Erfolg, sondern nur mit einer gewissen Wahrscheinlichkeit. Diese ist um so höher wenn schwache Passwörter verwendet werden. Bemerkenswert ist der für einen Wörterbuchangriff erforderliche, beängstigend geringe Aufwand! Als Beispiel sind hier die Daten bei Verwendung einer Liste aus dem OpenWall Projekt aufgetragen. Diese enthält 40 Mio Wörter und dazu Namenslisten aus mehr als 20 Sprachen und gängige Passwörter und Tastaturmuster (QWERTZUIO). Diese Methode wird immer bevorzugt verwendet, damit sind schon schwache Passwörter mit mehr als 40 Zeichen in kurzer Zeit geknackt worden, weil diese Zitate aus bekannten Büchern, Gedichten oder Filmklassikern waren!

Fazit

• Keinesfalls Wörter verwenden die in irgendwelchen Wörterbüchern oder Namenslisten vorkommen
, auch nicht Klingonisch!
• Lieber ein längeres Passwort als exotische Sonderzeichen
• Keine auch noch so langen Zitate oder Gedichte verwenden, auch wenn diese leicht merkbar sind
• die üblichen Ersetzungschemen (O->0 oder E->3) bringen nichts, die sind in guten Wörterlisten schon eingearbeitet
• Sonderzeichen sind nicht auf allen Gerätetastaturen vorhanden und sind somit evtl. einschränkend
• Bei der Softwareauswahl darauf achten dass zum Speichern von Passwörtern möglichst sichere Hashalgorithmen verwendet werden. Keinesfalls so etwas wie MD5 oder NTLM.

Wenn möglich ist die Verwendung eines Passwormanagers sinnvoll, zum Beispiel KeePassXC Damit ist die Verwendung sehr langer Passwörter handhabbar selbst wenn diese nicht-mnemonische Zufallsfolgen sind. Solche kann man übrigens auch sehr gut mit openssl selber erzeugen:

openssl rand -base64 32

LAENGE=32; openssl rand -base64 $((LAENGE*2)) |sed -e 's/[^[:alnum:]]//g' |cut -c -${LAENGE}

Skript Download

#!/usr/bin/gnuplot
#
#
#
size=5
array S[2*size]=["[0-9]",10.0,"[a-z]",26.0,"[a-z,A-Z]",52.0,"[a-z,A-Z,0-9]",64.0,"+Sonderzeichen",96.0]
# [0-9]            -> 10
# [a-z]            -> 26
# [a-z,A-Z]        -> 52
# [a-z,A-Z,0-9]    -> 62

# Energiebetrachtung: moderne NVIDIA Karte (2019) GTX 1080 leistet
#  25Mrd (25E12) MD5 /s oder 8,7 Mrd (8,7E12) SHA1 / s oder 6000 bcrypt hashes /s oder 35Mio ETH (ähnlich Keccak256 / SHA-3) Hashes
# 2023 leistet eine Nvidia CMP 170HX 164 Mio ETH (ähnlich Keccak256 / SHA-3) Hashes
# und ein Rechner verbraucht dabei ca 0,4kW
# davon lassen sich zum Beuispiel bis zu 4 Stück in einen PC einbauen dann läge man bei 1E14 /s
# Das Bitcoin Hash Netzwerk kann angeblich 69E18 SHA256 /s
CForce=35.0E6
P=0.4
EKosten=0.20
#Der Rechner kostet ca 1000 € Anschaffung und läuft vielleicht 5 Jahre
AKostenProTag=1000.0/5.0/365.0
# Damit kostet ein jeder Tag
EnergieProTag=P*24.0
KostenProTag=EnergieProTag*EKosten+AKostenProTag
CForceProTag=CForce*3600*24
#
set print 'Daten'
do for  [i=1:size] {
    Z=S[2.0*i]
    print "\"",S[2.0*i-1]," = ",Z,"\""
    do for [l=4.0:20.0] {
    N=Z**l
    print l," ",N," ",N/CForceProTag*KostenProTag
    }
	print ""
	print ""
}
set print "-"
#
# Farben definieren              R G B 
set style line  1 pi  2 lc rgb '#ffb000' lt 1 lw 1 # gold
set style line  2 pi  3 lc rgb '#ff0000' lt 1 lw 1 # red
set style line  3 pi  4 lc rgb '#0000ff' lt 1 lw 1 # blue
set style line  4 pi  5 lc rgb '#888888' lt 1 lw 1 # gray
set style line  5 pi  6 lc rgb '#808000' lt 1 lw 1 # yellow4
set style line  6 pi  7 lc rgb '#008080' lt 1 lw 1 # teal
set style line  7 pi  8 lc rgb '#b08040' lt 1 lw 1 #
set style line  8 pi  9 lc rgb '#4080b0' lt 1 lw 1 #
set style line  9 pi 10 lc rgb '#b08040' lt 1 lw 1 #
set style line 40 lc palette       lt 1 lw 1 #
#
set style line 17 pi 12 lc rgb '#4455bb' lt 4 lw 1 #
set style line 18 pi 12 lc rgb '#4455bb' lt 4 lw 1 #
set style line 19 pi 12 lc rgb '#4455bb' lt 4 lw 1 #
set style line 20 pi 12 lc rgb '#4455bb' lt 4 lw 1 #
set style line 21 pi 12 lc rgb '#800080' lt 1 lw 1 #
set style line 22 pi 12 lc rgb '#ffc000' lt 1 lw 5 # yellowgold
set style line 23 pi 12 lc rgb '#00ff00' lt 1 lw 1 # green
# Gitterdesign:
set style line 30 linetype 0 linecolor rgb "#707070"
set style line 31 linetype 0 linecolor rgb "#a0b0cf"
#
set xtics 1
set ytics 10 nomirror tc rgb '#ffc000'
set mytics 1
set grid xtics  back linestyle 30,linestyle 31
set grid mytics ytics  back linestyle 30,linestyle 31
set tics out
#set size 0.95,0.90
#set origin 0.03,0.03
set key title "Zeichenumfang"
set title "Brute-Force-Angriff auf Passwörter\nverschiedener Länge und Zeichenzahl" font ",18" textcolor rgb 'red'
set ylabel "Maximal benötige Brute-Force Versuche für sicheres Erraten des Passwortes"
set xlabel "Länge des Passwortes"
set logscale y
set logscale y2
set yrange [1E6:1e40]
set y2range [1E6:1e40]

set format y "%0.s %c"
set border
#
set terminal png size 1200,800
set output 'Passwortsicherheit.png'
set key top left
set y2label gprintf("Zeit zum Erraten bei %.0t·10^{%T} md5-hash-Berechnungen / s",CForce)
set y2tics out nomirror ('1 s' CForce, '1 h' 3600*CForce, \
'1 d' 24*3600*CForce, '1 Mo' 30*24*3600*CForce, '1 a' 365*24*3600*CForce, \
'100 a' 36500*24*3600*CForce, '1 Mio a' 1e6*365*24*3600*CForce, \
'1 Mrd a' 1e9*365*24*3600*CForce, '13.8 Mrd a' 13.8e9*365*24*3600*CForce)
#
plot for [i=1:size] 'Daten' index i-1 using 1:2 title columnhead with points ps 2 lw 2 axes x1y1, \
     40e6 title "übliche Wörter" axes x1y2

set output 'Passwortknackkosten.png'
unset y2tics
unset y2label
unset yrange
#set ytics 1000 nomirror tc rgb '#ff0000'
unset ytics
unset ylabel
set ytics out nomirror ('1 €' 1, '100 €' 100, '1000 €' 1000, '100 k€' 1e5,'1 M€' 1e6, \
'1 Mrd €' 1e9, 'weltweiter Goldbestand' 10e9,'4 B€, BIP DE' 4e12, '97 B€, BIP weltweit' 97e12, '1 000 000 000 B€' 1e21)
#
set format y "%0.s %c €"
set title "Kosten für einen erfolgreichen Brute-Force-Angriff auf ein Passwort\nje nach Länge und Zeichenumfang" font ",18" textcolor rgb 'red'
#set ylabel "Maximal benötigter Geldbetrag für sicheres Erraten des Passwortes"
plot for [i=1:size] 'Daten' index i-1 using 1:3 title columnhead with points ps 2 lw 2, \
40e6/9E17 title "übliche Wörter"