ISA Atmosphäre als Funktion
Die Normatmosphäre, Normalatmosphäre oder Standardatmosphäre ist ein Begriff aus der Luftfahrt und bezeichnet idealisierte Eigenschaften der Erdatmosphäre.
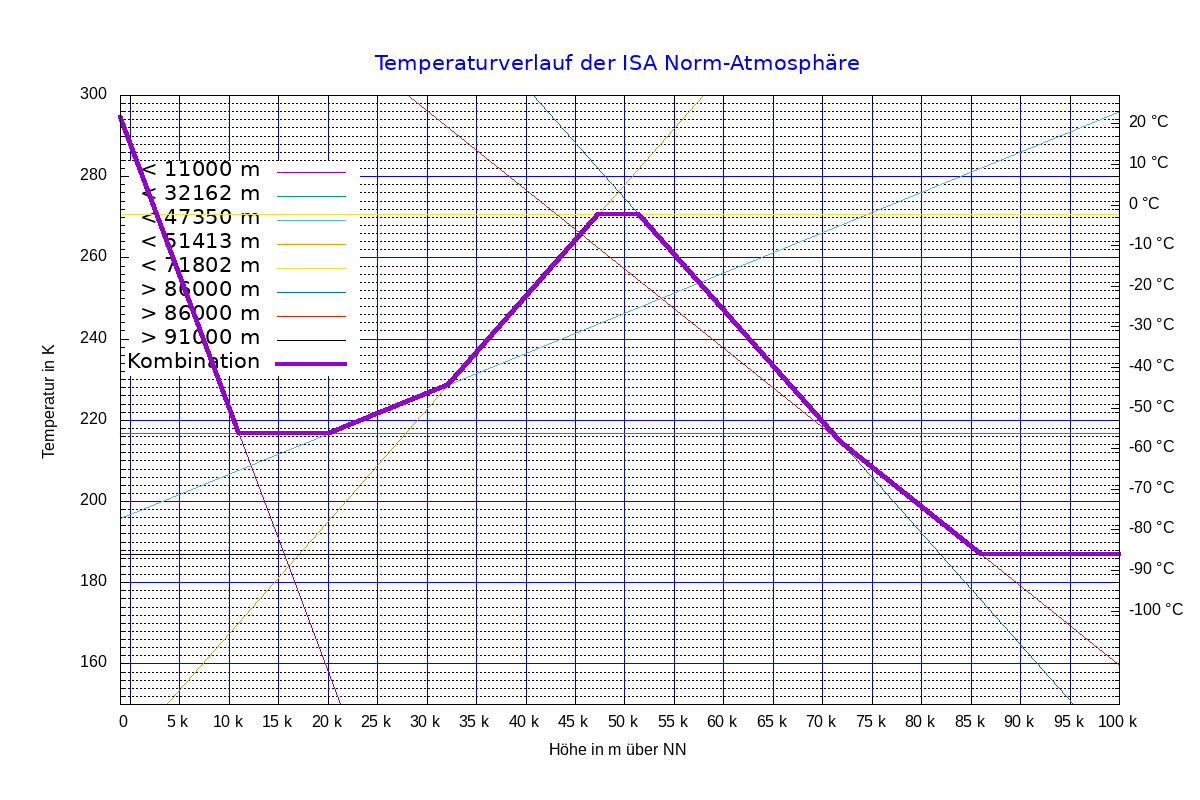
Die ICAO (International Civil Aviation Organization) hat 1976 mit ICAO-Dokument 7488[1] für die Luftfahrt eine allgemein gültige und verbindliche Normatmosphäre definiert. Der Temperaturverlauf mit der Höhe wird einer Tabelle definiert. Diese bilden also einzelne Funktionen die sich mit gnuplot einfach in eine einzige zusammanfassen lassen.
Skript-Download