Histogramm von Zufallszahlen

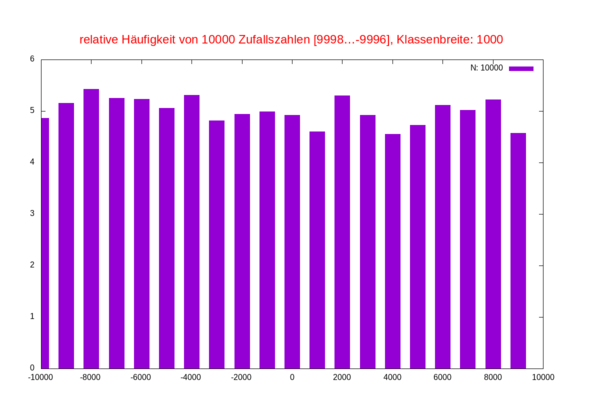
Eine einfache Untersuchung der Qualität von Zufallszahlen vergleicht die Häufigkeit bei der Einteilung in Klassen. Idealer Weise sollten diese in den Klassen gleichverteilt sein. Mit gnuplot kann man das auswerten.

gnuplot Skript Download

#!/usr/bin/gnuplot
# 2017-01-17, J. Schwender
# Gnuplot Skript zur grafischen Darstellung von Zufallszahlen
# Zahlenquelle: random.org
#
bw = 1000
set terminal png size 1200,800
set output 'random-statistics.png'
hist(x,width)=(width*floor(x/width))
set boxwidth bw*0.6
#set xtics 50
#set ytics 50
#set mytics 100
#set grid ytics mytics
set size 0.9,0.9
set origin 0.031,0.031
set style fill solid 1
stats 'random-numbers' prefix "A" ; N = A_records; ymax = A_max; ymin = A_min
set title sprintf("relative Häufigkeit von %.0f Zufallszahlen [%.0f…%.0f], Klassenbreite: %.0f", N, ymax, ymin, bw) \
    font ",18" textcolor rgb 'red'
plot 'random-numbers' u (hist($1,bw)):(1.0/N*100.0) smooth freq with boxes title gprintf("N: %.0f", N)

Zufallszahlen Skript Download

# getting random number from random.org
N=10000     # 1E4 is the limit!
Ymin=-10000
Ymax=10000
wget -O random-numbers \
 "https://www.random.org/integers/?num=${N}&min=${Ymin}&max=${Ymax}&col=1&base=10&format=plain&rnd=new"

Eine andere Untersuchung wie die Anwendung einer Autokorrelation ist mit gnuplot nicht so einfach möglich, das ist dann klar die Dmäne von anderen Programmen wie zum Beispiel GNU Octave wie in diesem Beispiel.

gnu octave Skript Download

#!/usr/bin/octave-cli --persist
% Zufallszahlen ergeben in einer Autokorrelation eine Dirac-Funktion
# Das kann man zum Testen der Qualität verwenden.
% ----------------------------------
pkg load signal;
addpath("~/octave");
y = importdata("random-numbers");
N = length(y)
sy = (sum(y)/N)^2
#
Zb = xcorr(y,y,'biased');
Zu = xcorr(y,y,'unbiased');
Zc = xcorr(y,y,'coeff');
#
fig = figure(1);
plot(y,"og")
title("Zufallszahlen von random.org",'FontSize',12)
grid on
#
fig = figure(2);
plot(Zb)
title("Autokorrelation von Zufallsreihen (biased)",'FontSize',12);
grid on
#
fig = figure(3);
plot(Zu)
title("Autokorrelation von Zufallsreihen (unbiaased)",'FontSize',12);
grid on
#
fig = figure(4);
plot(Zc)
title("Autokorrelation von Zufallsreihen (coeff)",'FontSize',12);
grid on
#
dtn=importdata("random-dt");
Nd=length(dtn)
[hdtn1,xdt1]=hist(dtn,Nd/100);
fig = figure(5);
plot(xdt1,hdtn1,"or") #,xdt2,hdtn2*10,"+b",xdt3,hdtn3*100,".y")
title("Histogramm der Differenzanalyse der Zufallszahlen",'FontSize',12);
#xlim([1 N*1.05]);
grid on
fig = figure(6);
plot(dtn,"or")
title("DifferenzZeitreihenanalyse der Zufallszahlen",'FontSize',12);
#xlim([1 N*1.05]);
grid on